|
||||||||
Дробово раціональні рівняння
Дробово раціональні рівняння
Розв’язання дробово раціональних рівнянь є не надто складним завданням, якщо Ви знаєте методику, а вона достатньо проста. Якщо рівняння має кілька доданків, то переносимо їх по одну сторону знаку рівності і зводимо до спільного знаменника. В результаті отримаємо дробову функцію f(x)/g(x), яка рівна нулю
Наступним кроком знаходимо корені чисельника. Відкидаємо серед них ті, що не належать області допустимих значень (нулі знаменника) і записуємо правильну відповідь. В теорії все досить просто, проте на практиці і в школярів, і в студентів виникають проблеми при зведені до спільного знаменника, відшуканні коренів і т.д. Для ознайомлення з розв’язуванням розглянемо декілька поширених завдань. Приклади дробово раціональних рівняньПриклад 1. Знайти корені рівняння
Розв’язання: За методикою переносимо доданки та зводимо до спільного знаменника
Прирівнюємо чисельник і знаменник до нуля і знаходимо корені. Перше рівняння можемо розв’язати за теоремою Вієта
Друге розкладаємо на множники
Якщо від коренів чисельника відкинути нулі знаменника, то отримаємо лише один розв’язок x=-7. Увага: Завжди перевіряйте чи співпадають корені чисельника і знаменника. Якщо такі є, то не враховуйте їх у відповіді. Відповідь: х=-7. ЧИТАЙТЕ ТАКОЖ: Поліном Лагранжа. Побудова в Maple------------------------------------ Приклад 2. Розв’язати рівняння
Розв’язання: Задано дробове раціональне рівняння. Знаходимо спочатку корені чисельника, для цього розв’язуємо квадратне рівняння
Обчислюємо дискримінант
та корені рівняння
Отримали три нулі чисельника Квадратне рівняння в знаменнику простіше і можемо розв’язати за теоремою Вієта
Чисельник і знаменник не мають спільних коренів тому всі три знайдені значення ------------------------------------ Приклад 3. Знайти корені рівняння
Розв’язання: Переносимо доданок за знак рівності
і зводимо до спільного знаменника
Розкриваємо в чисельнику дужки та зводимо до квадратного рівняння
Отримане дробово раціональне рівняння еквівалентне системі двох рівнянь
Корені першого обчислюємо через дискримінант
Нулі другого знаходимо без проблем
Виключаємо із розв’язків чисельника значення Відповідь: х=3. ЧИТАЙТЕ ТАКОЖ: Квадратне рівняння. Обчислення дискримінанту та коренів------------------------------------ Задачі на рухЗадача 4. Вертоліт пролетів за вітром відстань 120 км і в зворотньому напрямку повернувся назад, витративши на весь шлях 6 год. Знайдіть швидкість вітру, якщо швидкість в штиль становить 45 км/год. Розв’язання: Поділивши відстань на швидкість та просумувавши отримаємо час
Отримали дробово раціональне рівняння, схема розв’язування якого неодноразово повторювалася
Розв’язком другого рівняння будуть значення x=-45; x=45. Корені чисельника знайдемо після спрощень
Із фізичних міркувань перший розв’язок відкидаємо. Відповідь: швидкість вітру 15 км/год. ------------------------------------ Задачі на спільну роботуЗадача 2. Два лісоруби, працюючи разом, виконали норму вирубки за 4 дні. Скільки днів потрібно на виконання цієї роботи кожному лісорубу окремо, якщо першому для вирубки норми потрібно на 6 днів менше, ніж другому? Розв’язання: Нехай перший лісоруб виконує норму за х днів. Тоді другому необхідно (х+6) днів. Це означає, що за один день перший виконає Складаємо і розв’язуємо рівняння
Дане дробово раціональне рівняння еквівалентне системі двох рівнянь
Один розв’язок Відповідь: Роботу перший лісоруб виконає за 6 днів, а другий за 12. | ||
|
Схожі матеріали:
| ||
| Всього коментарів: 0 | |
|
ЗАРАЗ ЧИТАЮТЬ
|
|
|
 |  |
 |  |
 |  |
 |  |
 |  |


 Рівняння, які можна звести до дробу f(x)/g(x)=0 називається дробово раціональним рівнянням.
Рівняння, які можна звести до дробу f(x)/g(x)=0 називається дробово раціональним рівнянням.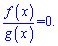
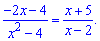
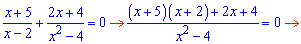
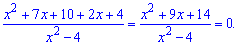
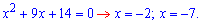
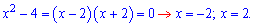
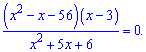
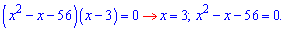
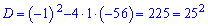
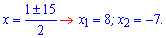
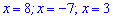 .
.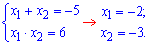
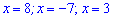 будуть розв’язками.
будуть розв’язками.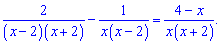
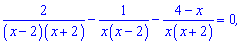
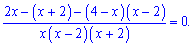
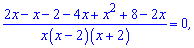
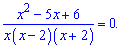
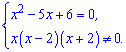
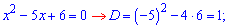
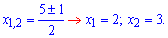
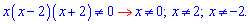
 і отримаємо.
і отримаємо.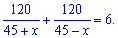
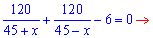
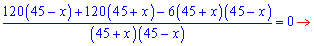
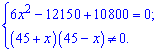
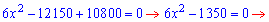
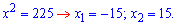
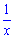 , а друга
, а друга 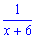 частину всієї норми. За умовою виконують норму за 4 дні, тобто обоє в день можуть виконати
частину всієї норми. За умовою виконують норму за 4 дні, тобто обоє в день можуть виконати 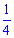 норми.
норми.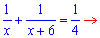
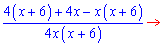
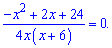
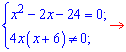
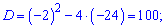
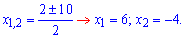
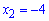 не відповідає фізичній суті завдання. Час другого лісоруба
не відповідає фізичній суті завдання. Час другого лісоруба